Publications | Jurijs Nazarovs

2023

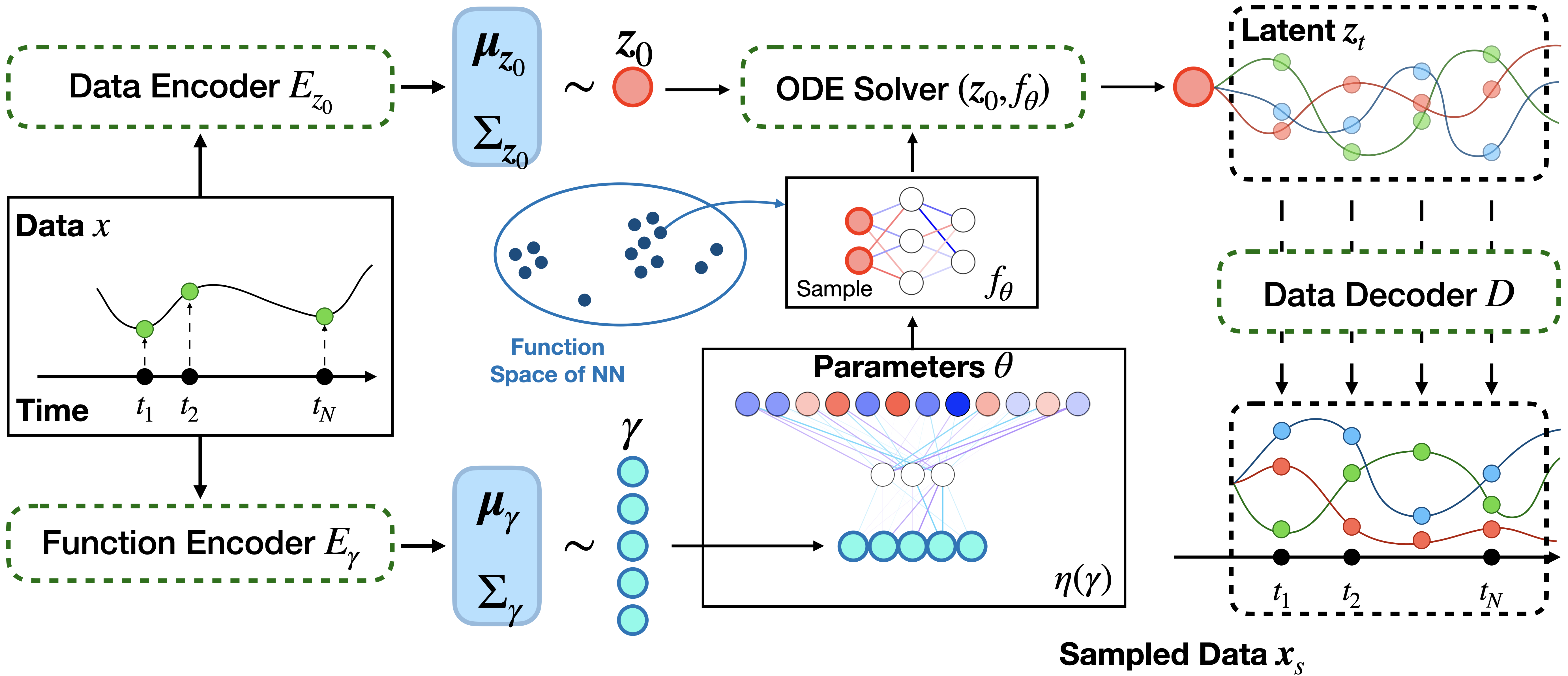
Variational Sampling of Temporal Trajectories

Nazarovs, Jurijs, Huang, Zhichun, Zhen, Xingjian, Pal, Sourav, Chakraborty, Rudrasis, and Singh, Vikas

arXiv - 2023

Abs arXiv

A deterministic temporal process can be determined by its trajectory, an element in the product space of (a) initial condition z_0 ∈Z and (b) transition function f: (Z, T) -> Z often influenced by the control of the underlying dynamical system. Existing methods often model the transition function as a differential equation or as a recurrent neural network. Despite their effectiveness in predicting future measurements, few results have successfully established a method for sampling and statistical inference of trajectories using neural networks, partially due to constraints in the parameterization. In this work, we introduce a mechanism to learn the distribution of trajectories by parameterizing the transition function f explicitly as an element in a function space. Our framework allows efficient synthesis of novel trajectories, while also directly providing a convenient tool for inference, i.e., uncertainty estimation, likelihood evaluations and out of distribution detection for abnormal trajectories. These capabilities can have implications for various downstream tasks, e.g., simulation and evaluation for reinforcement learning.

2022

Improving Robustness of VQA Models by Adversarial and Mixup Augmentation

Nazarovs, Jurijs, Peng, Xujun, Thattai, Govind, Kumar, Anoop, and Galstyan, Aram

arXiv - 2022

Abs PDF

Recent multimodal models such as VilBERT and UNITER have shown impressive performance on vision-language tasks such as Visual Question Answering (VQA), Visual Referring expressions, and others. However, those models are still not very robust to subtle variations in textual and/or visual input. To improve model robustness to linguistic variations, here we propose a novel adversarial objective function that incorporates information about the distribution of possible linguistic variations. And to improve model robustness to image manipulation, we propose a new VQA-specific mixup technique which leverages object replacement. We conduct extensive experiments on benchmark datasets and demonstrate the effectiveness of the proposed mitigation methods in improving model robustness.
Image2Gif: Generating Continuous Realistic Animations with Warping NODEs

Nazarovs, Jurijs, and Huang, Zhichun

AI4CC, CVPR - 2022

Abs arXiv Code Poster

Generating smooth animations from a limited number of sequential observations has a number of applications in vision. For example, it can be used to increase number of frames per second, or generating a new trajectory only based on first and last frames, e.g. a motion of face emotions. Despite the discrete observed data (frames), the problem of generating a new trajectory is a continues problem. In addition, to be perceptually realistic, the domain of an image should not alter drastically through the trajectory of changes. In this paper, we propose a new framework, Warping Neural ODE, for generating a smooth animation (video frame interpolation) in a continuous manner, given two ("farther apart") frames, denoting the start and the end of the animation. The key feature of our framework is utilizing the continuous spatial transformation of the image based on the vector field, derived from a system of differential equations. This allows us to achieve the smoothness and the realism of an animation with infinitely small time steps between the frames. We show the application of our work in generating an animation given two frames, in different training settings, including Generative Adversarial Network (GAN) and with L-2 loss.
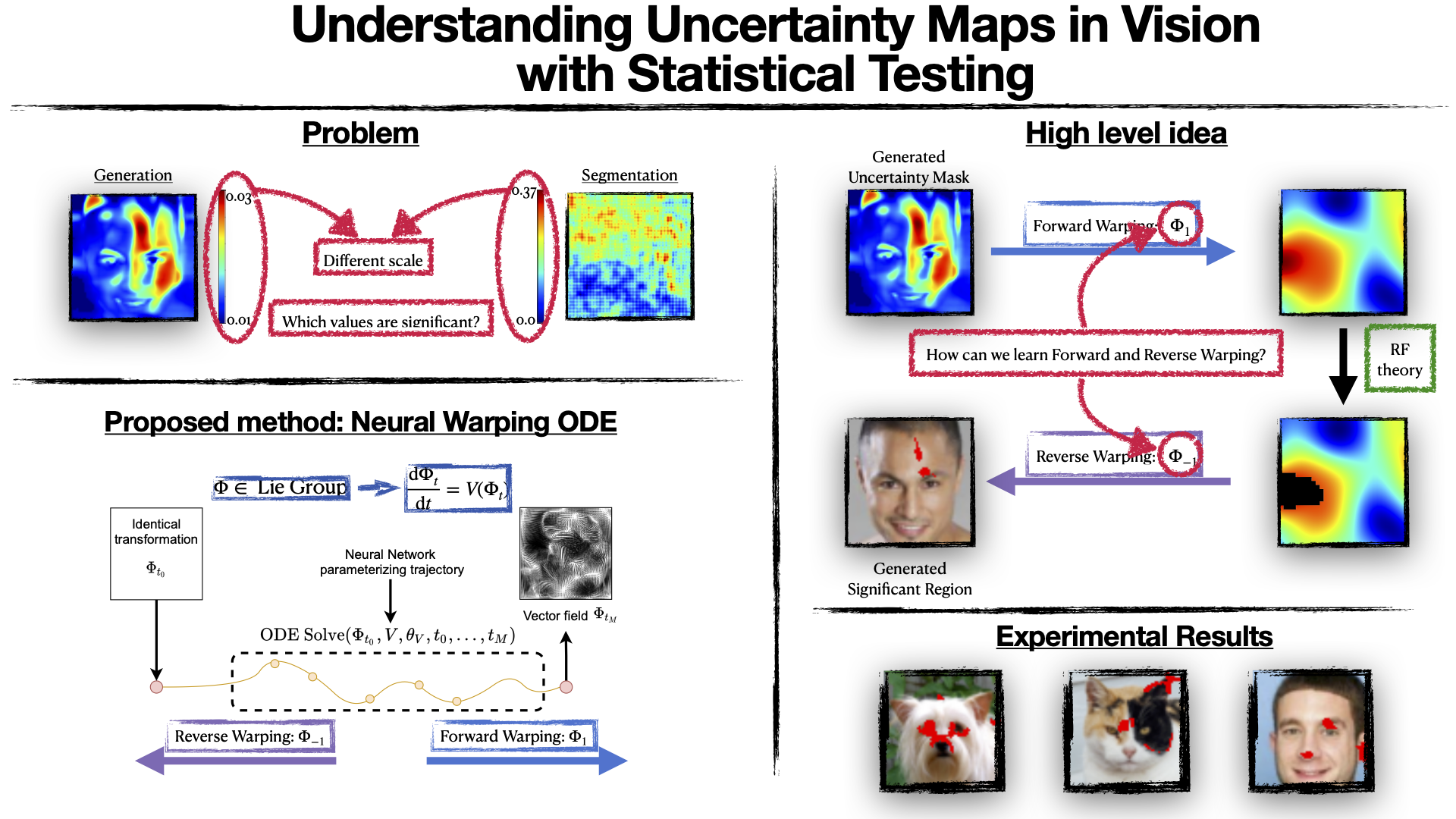
Understanding Uncertainty Maps in Vision With Statistical Testing

Nazarovs, Jurijs, Huang, Zhichun, Tasneeyapant, Songwong, Chakraborty, Rudrasis, and Singh, Vikas

CVPR - 2022 (Acceptance Rate: 25%)

Abs PDF Code Poster Video

Quantitative descriptions of confidence intervals and uncertainties of the predictions of a model are needed in many applications in vision and machine learning. Mechanisms that enable this for deep neural network (DNN) models are slowly becoming available, and occasionally, being integrated within production systems. But the literature is sparse in terms of how to perform statistical tests with the uncertainties produced by these overparameterized models. For two models with a similar accuracy profile, is the former model’s uncertainty behavior better in a statistically significant sense compared to the second model? For high resolution images, performing hypothesis tests to generate meaningful actionable information (say, at a user specified significance level 0.05) is difficult but needed in both mission critical settings and elsewhere. In this paper, specifically for uncertainties defined on images, we show how revisiting results from Random Field theory (RFT) when paired with DNN tools (to get around computational hurdles) leads to efficient frameworks that can provide a hypothesis test capabilities, not otherwise available, for uncertainty maps from models used in many vision tasks. We show via many different experiments the viability of this framework.
Radial Spike and Slab Bayesian Neural Networks for Sparse Data in Ransomware Attacks

Nazarovs, Jurijs, Stokes, Jack W., Turcotte, Melissa, Carroll, Justin, and Grady, Itai

arXiv - 2022

Abs arXiv
Ordinal-Quadruplet: Retrieval of Missing Classes in Ordinal Time Series

Nazarovs, Jurijs, Lumezanu, Cristian, Ren, Qianying, Chen, Yuncong, Mizoguchi, Takehiko, Song, Dongjin, and Chen, Haifeng

arXiv - 2022

Abs arXiv

In this paper, we propose an ordered time series classification framework that is robust against missing classes in the training data, i.e., during testing we can prescribe classes that are missing during training. This framework relies on two main components: (1) our newly proposed ordinal-quadruplet loss, which forces the model to learn latent representation while preserving the ordinal relation among labels, (2) testing procedure, which utilizes the property of latent representation (order preservation). We conduct experiments based on real world multivariate time series data and show the significant improvement in the prediction of missing labels even with 40% of the classes are missing from training. Compared with the well-known triplet loss optimization augmented with interpolation for missing information, in some cases, we nearly double the accuracy.

2021

Mixed Effect Neural ODE: A variational approximation for analyzing the dynamics of panel data

Nazarovs, Jurijs, Chakraborty, Rudrasis, Tasneeyapant, Songwong, Ravi, Sathya, and Singh, Vikas

UAI - 2021 (Acceptance Rate: 26%)

Abs PDF Code Poster Video

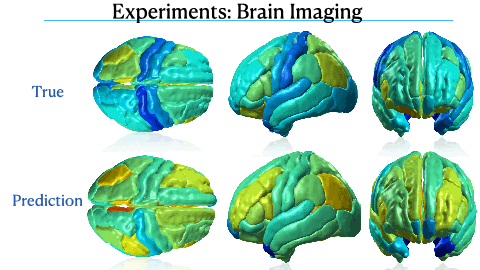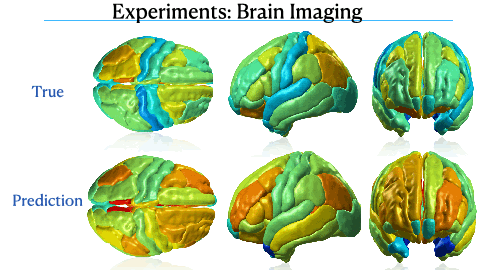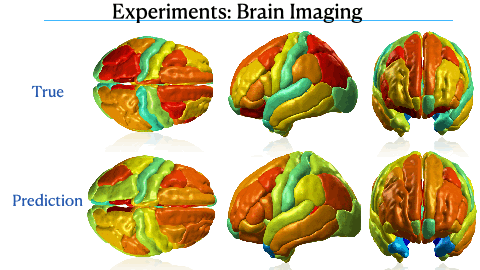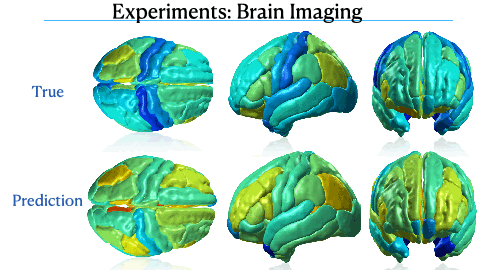
Panel data involving longitudinal measurements of the same set of participants or entities taken over multiple time points is common in studies to understand early childhood development and disease modeling. Deep hybrid models that marry the predictive power of neural networks with physical simulators such as differential equations, are starting to drive advances in such applications. The task of modeling not just the observations/data but the hidden dynamics that are captured by the measurements poses interesting statistical/computational questions. We propose a probabilistic model called ME-NODE to incorporate (fixed + random) mixed effects for analyzing such panel data. We show that our model can be derived using smooth approximations of SDEs provided by the Wong-Zakai theorem. We then derive Evidence Based Lower Bounds for ME-NODE, and develop (efficient) training algorithms using MC based sampling methods and numerical ODE solvers. We demonstrate ME-NODE’s utility on tasks spanning the spectrum from simulations and toy datasets to real longitudinal 3D imaging data from an Alzheimer’s disease (AD) study, and study the performance for accuracy of reconstruction for interpolation, uncertainty estimates and personalized prediction.
Graph reparameterizations for enabling 1000+ monte carlo iterations in bayesian deep neural networks

Nazarovs, Jurijs, Mehta, Ronak R., Lokhande, Vishnu Suresh, and Singh, Vikas

UAI - 2021 (Acceptance Rate: 26%)

Abs PDF Code Poster Video

Uncertainty estimation in deep models is essential in many real-world applications and has benefited from developments over the last several years. Recent evidence suggests that existing solutions dependent on simple Gaussian formulations may not be sufficient. However, moving to other distributions necessitates Monte Carlo (MC) sampling to estimate quantities such as the KL divergence: it could be expensive and scales poorly as the dimensions of both the input data and the model grow. This is directly related to the structure of the computation graph, which can grow linearly as a function of the number of MC samples needed. Here, we construct a framework to describe these computation graphs, and identify probability families where the graph size can be independent or only weakly dependent on the number of MC samples. These families correspond directly to large classes of distributions. Empirically, we can run a much larger number of iterations for MC approximations for larger architectures used in computer vision with gains in performance measured in confident accuracy, stability of training, memory and training time.